果たして数学はヒトの教育に必要不可欠なものか。
現役の数学教師である私の答えはノーです。
もしヒトの成長に数学が必要不可欠というのであれば、近代教育の普及していない国は未熟者だらけだと言っているのと同じ。
世の中にはそのような考え方もあると思いますが、私自身の信条としてその手の偏見に与するつもりはありません。
たまたま数学が得意だった私個人の実感として言わせていただければ、数学はグルメや読書や和太鼓などと並ぶ趣味の一環。
脳をフル回転させる充実感を味わうための、単なる娯楽の一つです。
ですが、どのような娯楽を好むかという趣向は人によってそれぞれ違いますから、単一のカリキュラムを強いる現在の日本の教育システムは数々の我慢とストレスを生むことになります。
数字や計算などに全く興味が持てない人にとって、学校で数学をやらされるのはまるで拷問のような体験でしょう。
では何故数学なんてものが、近代の教育システムに取り込まれているのか。
それは、私たち個人にとっての幸せのためではなく、私たちを取り巻くこの近代社会を成り立たせるためです。
私たちが当たり前に暮らしているこの近代社会の根幹には、近代合理主義という価値観が隠れています。
近代合理主義とは、精霊や悪霊や神などを無根拠に信じ込む態度が非合理的だと貶められ、科学的な態度こそが合理的だと持て囃される世の風潮のこと。
そして、この近代合理主義を支える支柱となっているのが数学という学問なのです。
私たちが学校で数学を強制されているのは、そうすることで数学という学問の権威を保ち、近代合理主義という固定観念を再生産していくため。
そこで今回は、数学という学問が占めるこの特異なポジションの由来について検証してみます。
そのためにまず、 京都大学の上野健爾氏が『こんな入試になぜできない、大学入試「数学」の虚像と実像』という著書の中で述べている数学の特徴についての文章を紹介したいと思います。
一時間しか数学を教える時間がないとき、あなたは数学の何を高校生に伝えたいか。
それぞれの数学観によって、教える内容は違ってこよう。
どこを強調するかは違うにしても、次のことのいくつかはどうしても伝える必要があるという点では多くの人が賛同するであろう。
①数学ではひとたび証明された正しい事実は、時代や社会に関わらず常に正しい。
(ニュートン力学が原子の世界では適応できないことと学問の性格が違う)
②数学は論理に基づいて理論が展開され、数学で使われる多くの記号も含めて、共通の言葉として全世界で通用する。
③数学は抽象的な表現をとることが多い。
抽象化された概念は多くの内容を含んでいる。
たとえば、文字式はたくさんの内容を含んだ言葉である。
④数学は現代の科学を支える有用な学問であるとともに、人間の精神活動のなかで美をもたらす学問である。
⑤数学の歴史は考え方の歴史であり、既成概念から自由になる歴史でもある。
ここでは最初に「数学ではひとたび証明された正しい事実は、時代や社会に関わらず常に正しい」という性格が挙げられていますが、「時代や社会に関わらず常に正しい」というのはかなりの強気な発言です。
数学者が自信をもってこのように言える根拠はどこにあるのでしょうか。
「ニュートン力学が原子の世界では適応できないことと学問の性格が違う」とありますが、その性格の違いとは何なのでしょうか。
数学だけに許された特権というものがあるのでしょうか。
私は、この性格の違いが「現実世界のことを語るかどうか」にあると考えています。
医学・生物学・化学・物理学…いろんな学問に世の仕組みを説明するいろんな理論が存在しますが、それらは「もしそうなら辻褄が合う」という予想の積み重ねであって「なぜ現実世界がそうなっているのか」という問いにきちんと答えられるものではありません。
いいや、科学は世の中の仕組みをきちんと説明できているという人もいるかもしれませんが、科学において 「・・・であることが証明された」と言うとき、根拠としているのは予想した仮説に合致する実験や観測の結果がいくつか出たということに過ぎません。
しかし、現実世界のすべての可能性を調べつくすことなんてできませんから、仮説に合う実験結果が何億何兆出ようともその仮説が普遍的な真理であることの証明にはなりません。
現実世界のどこかに反例があってまだ観測者が見つけていないだけかもしれないのです。
だから、そういった現実世界のことを語った理論というのはいつ覆ってもおかしくない性格のものですし、「ニュートン力学が原子の世界では適応できない」というような事態も当然のように起こりうるわけです。
その点数学はどうなのか。
ここは思想や立場によって意見が分かれるところですが、私個人の意見としては、数学とは現実世界のことを語る学問ではなく、公理という基本ルールを仮定することで組み立てられたゲームの世界のお話です。
だから、ゲーム内でのお話が正しいかどうかは最初に決めた約束ごとに則っているかだけを検討すればよいので、そのルールを尊重する限りにおいては「時代や社会に関わらず常に正しい」ということも言えると思っています。
数学の仕事はルールに即したゲームを作ること。
「現実世界を語るのにどんなゲームをモデルとして採用すればよいか」と考えるのは科学の側の問題であって数学自身の問題ではありません。
つまり、他の学問にない数学の特権とは「現実世界のことを語る必要がない」という学問の性格のことなのです。
ですがそれでも、「数学ではひとたび証明された正しい事実は、時代や社会に関わらず常に正しい」という言い方で数学を説明することに、私はあまり賛成できません。
数学で語られる正しさはあくまでも【ある公理系をルールとして認めた世界での】というカッコつきの正しさであり、そこの部分を省いて説明してしまえば、数学で語られることがまるでこの現実世界での普遍的な真理であるかのような印象を与えてしまうかもしれませんから。
しかし、「数学で語られることはこの世の普遍的な真理だ」と誤解される状況は、「数学で語られる正しさがカッコつきの正しさでしかない」とバレてしまう状況に比べて、真理という付加価値の分だけ数学という学問の魅力が底上げされます。
数学者や数学教師の立場からすれば、自分たちが居座っている「数学従事者のピラミッド」の権威を守っていくためにも、数学がより高尚なものだと見なされて欲しいと願うのは当然の成り行きです。
つまり、カッコつきの正しさという部分については黙っておいたほうが数学という学問のイメージ戦略上有利に働くのです。
また、その他の科学もこの数学のイメージ戦略に乗っかっています。
「数学は科学の女王にして奴隷」という言葉にもあるように、数学は他の科学から女王のように敬意を払われながらも奴隷のように良いように利用されているという両面があります。
数学は、「時代や社会に関わらず常に正しい」とかっこ付きでも言えるその独自のポジションから「この世の普遍的な真理」という付加価値にもっとも近い学問として、他の科学からも一目置かれる存在となっています。
それと同時に、数式を利用している多くの科学には、数学の持つ特殊な威光をそれぞれの学問のイメージ戦略に流用しようとする嫌いがあります。
それぞれの分野の理論を数式で現すことにより、「こんな綺麗な数式で表せるということはこの世の普遍的な真理である可能性が高い」といった幸せな誤解が生まれることを、暗に期待しているという側面が少なからずあるわけです。
こういった「原子力ムラ」ならぬ「真理ムラ」とも呼べるズブズブの利害関係が存在している以上、「数学ではひとたび証明された正しい事実は、時代や社会に関わらず常に正しい」という曖昧な説明の仕方はまだまだ生き残っていくだろうと思います。
では、カッコつきではない正しさとはどこに在るのか。
私の見解では、言葉はそもそも記述ではなく説得のために存在しており、「正しさ」という概念は説得のために編み出された方便の一つでしかありません。
「こちらが正しい」とか「何が正しいのか分からない」とか「本当の正しさなんてどこにもないじゃないか」などと本気で訴えている人は、その方便を真に受けた挙げ句、真理ムラを養護する勢力の一部となっているわけです。
誤解されると困るのですが、私は数学やその他の科学を忌み嫌っているわけではありません。
むしろその逆で、単純な知的好奇心から多大なる興味や感心を持っています。
ただ、数学や科学の周辺にうようよと棲息している「真理」「正しさ」「記述」といった信仰を押し付けたがっている勢力を疎んでいるだけなのです。
上野健爾氏の説明する数学の5つの特徴の中で、私がもっとも共感しているのは、「数学の歴史は考え方の歴史であり、既成概念から自由になる歴史でもある」という最後の指摘です。
私は「ものごとの状態や事実を記述するために言葉が存在する」というのは説得のために造られたフィクションであり、社会通念によって刷り込まれてきた固定観念だと考えています。
そういった既成概念から自由になれたのは、まさに数学の世界で発想力を養ってきたから。
そのおかげで私自身は20代前半の頃に真理ムラから距離を置くことができたわけで、数学という存在は私自身の支柱にすらなっています。
たとえ数学に「真理」という威光がなかったとしても、数学が持っている「考え方の歴史」は趣味として十分魅力的ではないでしょうか。
※当ブログの主なテーマは、この世界を支配する「正しさ」という言葉のプロレスとの付き合い方。
mrbachikorn.hatenablog.com
「正しさ」というゲームの最大の欠陥は、何を「正しい」とし何を「間違ってる」とするのかというルールや、その管理者たるレフェリーが、実際にはどこにも存在しないということ。
人類はこれまで数え切れないほどの論争を繰り広げてきましたが、それらのほとんどは「レフェリーの代弁者」という場を仕切る権限をめぐっての権力闘争でした。
「レフェリーの代弁者」という立場は、自分の個人的な要求でしかない主張を、まるでこの世の既成事実のように見せかけるための隠れ蓑です。
「それは正しい」とか「それは間違ってる」という言い方で裁きたがる人たちは、私はこの世のレフェリーの代弁をしているだけなんだという迫真の演技で己の発言の圧力を高めていたのです。
演技の迫力とは、演技者が役にどれだけ入り込めるかで決まるもの。
人々はいつしかレフェリーの代弁者のふりが説得のための演技であったことを忘れ、「どこかに本当の正しさがあるはず」といった物語を本気で信じこんでしまいます。
こうして人類の間には、「正しさ」という架空のレフェリーの存在をガチだと捉えてしまう、大がかりなプロレス社会が成立していきました。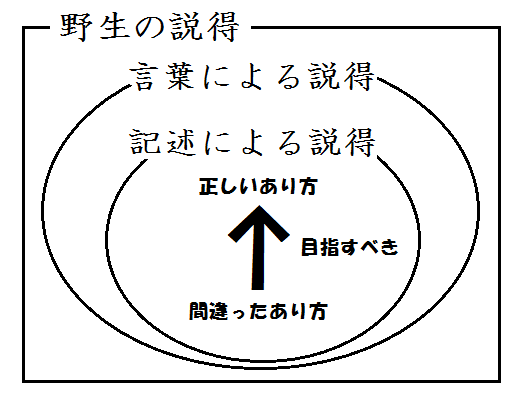
そのプロレス的世界観を支えている固定観念の源を「記述信仰」と名付けました。
以下の記事では、この「記述信仰」の実態を上のような簡単な図まとめて解説していますので、ぜひご一読ください。
